GranoMetry™ Blog
Updated 2010-08-19 15:12
Dear colleagues,
I present this Blog in order to show Sand Texture Sedimentology, STS, in a new light. I invite registered users to discuss any subject from this field. I devoted my life to rehabilitate it, particularly after the Robert Ehrlich’s killing Editorial in Journal of Sedimentary Petrology (53/1983, No. 1/March, p. 1). I had to agree with him. My life task was to make away with the reason of that disaster, in my opinion caused by two main errors:
- poor instruments (sieves and inexpensive settling tubes),
- inappropriate statistical techniques (seeking magic in skewness & kurtosis).
Synonyms related to grain (size):
- Gaussian distribution = normal distribution
- Grain common for sand ~ particle general term for any size, but unusual for gravel and coarser
- Granularity includes also size-related properties such as sedimentation velocity ~ dispersity exact & more specific than granularity
- Sedimentation ~ settling¨mass (collective) sedimentation
- Velocity = rate with a vector
- Nominal diameter = diameter of the volume equivalent sphere
type of equivalence: = equal ~ approximate
… A grain: what is it?
The tradename GranoMetry™ consists of the Latin word granum = grain, and the Greek word metron = to measure. A grain (particle) is a solid body, of an irregular shape. In this Blog, we will mainly discuss grains of natural sand. Their shape is not only irregular, but also randomly different. Typically, grains consist of one or a few minerals, most often quartz, sometime calcite, but also – such as green sands on Hawaiian Islands – of olivine, augite, hornblende, magnetite, feldspars, without any quartz.
Sedimentation velocity versus grain size
Sand, a seemingly prosaic item, may have immense value. The sand sedimentation velocity distribution components may be related to processes, which, as they formed the sand, also formed, or provided reservoirs for, petroleum, gas, and some valuable minerals. The sands' value may result not only from some important minerals but also from the sands' availability, where we do not like it, such as in harbors, ports and waterways, and elsewhere from its vanishing from places we like it, such as beaches.
Granularity (dispersity) is the fundamental property of granular materials. In sands, grain size has descriptive and sedimentation velocity genetic value. Until now, of granularity features, mostly grain size has been used, and, unfortunately, not only for classification but also for genetic interpretation, for which it is quite unsuitable. In addition, grain size definition and measuring are related to several problems.
Grain size problems
Microscopic (optical) sizing has accuracy limitations. We do not see grain size correctly. In order to measure the sand grain size and magnify its image by microscope, the angle of the rays’ convergence grows with the magnification. This is why we do not focus onto the maximum, but to about up to 27% smaller projection. More complicated is the apparent size reduction in thin sections, the 0.03 mm thin slices of rocks. The random cuts of large grains are about 27% smaller on average. However, the thin sections cut finer grains (as fine as the slice thickness or smaller) seldom or not at all. We are viewing the fine grains in projections close to the “correct” grain size. However, projections are only 2-dimensional pictures of the grain – a 3-dimensional body. We are losing one dimension!
Sieving has almost no value because:
- Sedimentation velocity can not be correctly calculated from the sieve grain size;
- too wide intervals (0,25 PHI instead of 0.02 PHI), too few fractions in sand range (25 instead of >400);
- grain shape affects the sieve grain size inconsistently with sedimentation velocity: sieves measure non-spherical grains coarser but they settle slower and have greater specific surface;
- sieving is time consuming and inaccurate.
Sieving can hardly meet the accuracy requirements, woven sieves not at all. They can easily become defective by an almost invisible shift of a wire, which may enlarge some openings. We should prefer micro precision sieves with circular holes (e.g. by VECO, produced by galvanic deposition on thin nickel plates, accuracy ±1 micron), support the sieving by a liquid (alcohol), use vibration in random 3D-directions and monitor it up to constant weight to check whether there are still some grains to pass. On screens with holes finer than about 0.2 mm, the load should not exceed 0.3 g/cm2 for each screen, because each grain must get a chance to be measured, i.e., it must “wait” in maximum 10 layers. A 20-gram sand sample may be sieved on 8 screens for 8 hours; ultrasound cleaning and microscopic checking of sieves may take more than one hour.
A grain size definition includes grain shape, which is irregular and randomly different in natural sands. However, one may eliminate the shape influence on the size by using the diameter of a volume equivalent (nominal) sphere. Because the volume measurement of sand particles is difficult and inaccurate, we should define the grain size as the size of a sedimentation velocity equivalent geometric body. Usually, a sphere has been chosen as such a body.
Because a sphere sediments much faster than a naturally shaped volume equivalent sand particle, Jiri Brezina (1979) suggested the hydraulic equivalence to a rotational ellipsoid with the typical Corey’s Shape Factor value, SF = 0.65. He also developed the converting equations and the most precise Sand Sedimentation Analyzer™.
We usually know exactly all variables needed to solve the converting equations: the grain material and thus its mass per volume, density, and the laboratory gravity acceleration. The grain mass is perfectly sensed by acceleration as a buoyant force (weight) resisted by a fluid frictional force in an equilibrium at the terminal sedimentation velocity. The Analyzer measures the sedimentation time in milliseconds over the sedimentation length of 180 cm and calculates the fluid density and viscosity from the water temperature measured to ± 0.1°C. Sand grains in water accelerate sufficiently by gravity to sediment separately.
For genetic interpretations in sedimentology, the most precise distribution data are needed to decompose them into up to 5 Gaussian components. These components help reconstruct recent and fossil streams, which deposited them, trace the sand transport etc., because they control the location of each grain during its deposition we found it = the sediment origin. Sedimentation velocity describes the grain size most accurately. The sedimentation velocity of sand grains is more related to their deposition (origin) than their size. |
Petrology of Sedimentary Rocks by
Robert L. FOLK, 1980 (internet edition 1981)
Recently, I read the latest edition of the popular book by Robert Folk in the Internet. I was disappointed by about 8 lines of his text on Settling Tubes. I immediately called Bob and asked him to exchange his text with that which I had sent him by eMail. However, he replied that the geology librarian he had consulted was strongly against any change: “even if it is an electronic version, the date is 1980 without further emendations and it would be very non-kosher to change any part of it retroactively“. Of course, this was not my intention, I wanted him to write his current comment quoting me. But Bob encouraged me to publish my text independently of his book. I would like to make clear that a sand granularity has value for sedimentologic interpretations only if made extremely accurately and properly described. This requirement alone gives no chance to rapid sieving and any type of “inexpensive” settling tube.
Please compare his text (red print below) with my suggestion (green print farther below) and tell me.
Size Analysis by Settling Tube
by Robert L. Folk, 1980 (Internet edition 1981)
For rapid, generally less accurate work, grain size of sand may be measured by settling the grains through a water column. Fancy devices are available to make sure all the grains start settling together. Best results are obtained with water columns at least 10 cm. in diameter, and with a small number of grains. Results are recorde continuous weighing of grains accumulating at the bottom, or by automatic recording of pressure differences. Both “sievers” and “settlers” are strongly opinionated as to which is the best method of measuring grain size -- one may just as well ask, “Which is the best way of doing carpentry - a saw or a hammer?”
Size Analysis by Settling Tube
by Jiri Brezina (2009)
For rapid and most accurate work, granularity of sand measured by settling of grains through a water column, can reach the highest accuracy of all sizing methods, if the following terms are fulfilled:
- water column about 20 cm in diameter, sedimentation length about 180 cm;
- small sample size: 15,000–20,000 grains;
- sediment sensed by an underwater electronic balance with a high S/N (signal to noise) ratio (>80 dB) & fast response (<0.02 second).
The above sample size is statistically representative and reduces an initial density streaming to acceptable minimum. For that purpose, the sample introduction device homogenizes the upper 5 cm of the suspension by eccentric rotation and vibration of the Venetian blind lamellae.
The continuous weighing at the bottom must be fast
(>96 % of load recorded within <20 milliseconds) and sensitive (<0.01
milligram resolution). Such a balance must be well insulated from
environmental vibration (the tube suspended on shock absorbers).
The electronic weight output signal must be “high fidelity”, i.e. with a
high S/N (signal to noise) ratio (>80 dB). In order to collect optimum
number of measurements (weighing signal samples), the sampling scheme
must follow at constant intervals of a logarithmic sedimentation
velocity, 0.02 PSI. In order to reduce the signal noise further, the
voltage must be digitized by a fast integrating 16 bit ADC
(Analog/Digital Converter), delivering >1000 measurements per second.
These data are averaged over the non-linear time intervals (a simple
mathematical signal filter).
Meeting these requirements can never be expected from “inexpensive” settling tubes, such as those sensing a suspension pressure difference. Results of the users of my advanced settling tubes (European colleagues mostly) confirm the words R. L. FOLK wrote 1962: "The fault, dear Friends, lies not in the sands, but in your tubes, that they are skewing things." The “inexpensive” settling tubes have discredited grain size interpretation, which has also suffered from taking values and/or “polarity” of unsuitable distribution parameters skewness & kurtosis as a magic key.
Joe R. CURRAY (1960) in his pioneer work “Tracing sediment masses by grain size modes” demonstrated the best common sense interpretation of natural size distributions: he decomposed them into normal (Gaussian) components and used them as natural tracers. In his time without computers, he worked graphically. Tjeerd Jerry van ANDEL (1973) could decompose by a special analog DuPont Curve Resolver. Unfortunately, no other sedimentologist had this expensive device available, DuPont stopped its production & support from economic reasons. Because the graphical decomposition is time-intensive and inaccurate, Curray’s idea could not be further used before J. Brezina constructed his advanced settling tube and adapted a stable decomposition program by Isobel CLARK (1977) for his MacroGranometer™ system.
Therefore, the most effective interpretation of natural distributions must be based on the three parameters (mean, spread and component percentage or proportion) of each normal distribution component. In studies based on decomposition of the observed distributions into a few Gaussian components, the highest analytical accuracy is inevitable. The mixing of normal distributions should be understood as either of different materials or of different processes.
In clastic deposits, do we really need grain size? A grain non-sphericity may so much reduce the hydrodynamically equivalent sphere size that the grain may become classified into a category sedimenting under another hydrodynamic regime. Instead of the grain size, we actually need the grain settling rate PSI, which eliminates the problem of particle shape.
A conversion of a normal (Gaussian) PSI sedimentation velocity distribution into a PHI grain size distribution generates a different standard deviation and negative skewness of the PHI distribution. Jiri BREZINA (1963) showed graphically that these changes result from the Kapteyn’s transformation. His original data, based on limited resources known to him (Russian publications), had to be replaced by more reliable ones as in his equation (1979). Both the changes (S.D. and SK) depend not only on the PSI mean and SD values but also on the Shape Factor values used for the conversion.
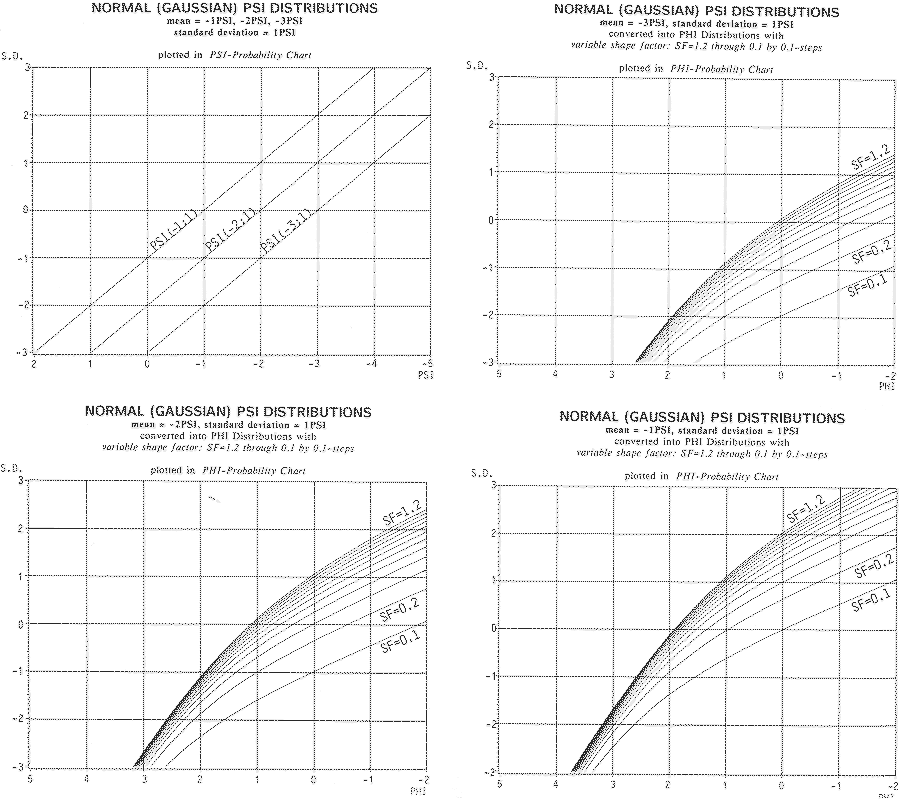
| Fig. 1: Probability plots of three normal PSI distributions (from top left: a, b, c, d). The Y-axes are in Standard Deviation units (S.D.). 1a: The PSI probability chart displays the normal PSI distributions as three straight lines. They have different mean values (-1, -2, -3 PSI) but the same standard deviation (SD) value (1 PSI) so that they are parallel.Figs. 1b – 1d show the probability plots of the converted PHI distributions. They are no more straight but curved displaying different PHI-standard deviation and different negative PHI-skewness. Each conversion was performed for 14 SF values (SF = 1.2, through SF = 0.1 at 0.1 steps) giving 14 PHI distributions (curves).. |
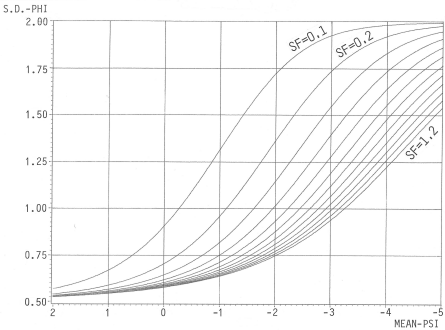
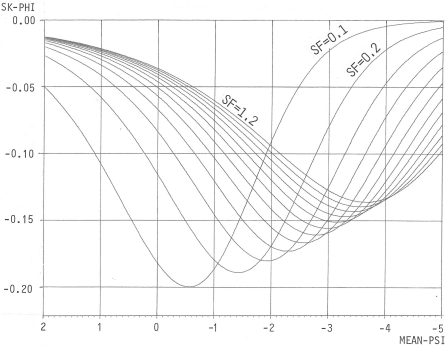
| Fig. 2: Standard Deviation (SD) of PHI distributions formed by the conversion from a PSI normal (Gaussian) distribution with various SF values. | Fig. 3: Skewness (SK) of PHI distributions formed by the conversion from a PSI normal(Gaussian) distribution with various SF values. |
Sand Sedimentation Analyzer™
J. Brezina has devoted half a century to Sand Texture Sedimentology. He critically evaluated several thousand data and summarized them into a generally valid equation for the drag coefficient as a function of Reynolds’ number and Corey’s Shape Factor of sedimenting grains. This equation provides a consistent mathematical basis for the sedimentation velocity – particle size, shape and density conversions and should be used instead of the popular equation by Ronald J. GIBBS, Martin P. MATTHEWS & D. A. LINK (1971) for spheres, which neglects one polynomial part to be quadratic and is therefore inaccurate.
His Sand Sedimentation Analyzer™ meets the above requirements and becomes standard in prominent European institutions, such as:
- Marine Science Department, Senckenberg Institute, Wilhelmshaven, Germany;
- Geology Department, Vienna University, Austria;
- Oceanographic Department, University of Faro, Portugal;
- Geographic Department, University of Kopenhagen, Denmark;
- Geological Department, University of Trieste, Italy.
His ideas will be incorporated into the international ISO standards in 2010.
JB has developed the unique Sand Sedimentation Separator™ (the prototype for Geomar, Research Center for Marine Geosciences, University of Kiel, Germany) isolating up to 25 programmable settling velocity fractions. Sedimentational separations from narrow sieve fractions continuously and rapidly isolate porous microfossils, such as Foraminifera, and heavy minerals, much more accurately than with heavy liquids, which are mostly poisonous.